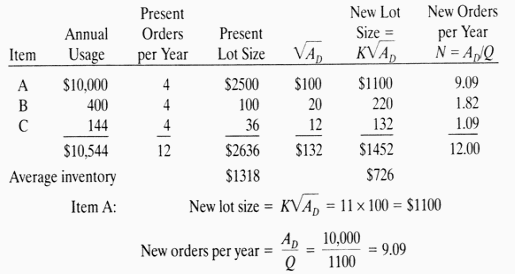
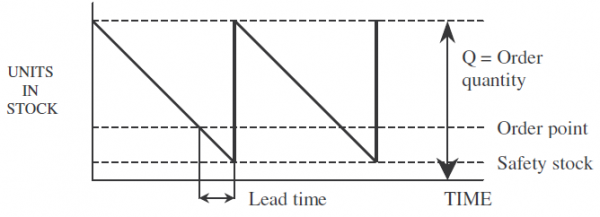
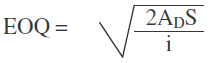Objectives of Inventory
A firm wishing to maximize profit will have at least the following objectives :
- Maximum customer service,
- Improving Operating efficiency by
- Low-cost plant operation,
- Minimum inventory investment.
Customer service
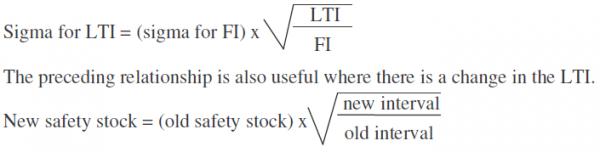
In inventory management, the term is used to described the availability of items when needed an is a measure of inventory management effectiveness. Inventories help to maximize customer service by protecting against uncertainty. Demand and lead time to get an item are often uncertain, possible resulting in stockouts and customer dissatisfaction. For these reasons, it may be necessary to carry extra inventory, called safety stock.
Delivering in a Timely Manner : The need to provide quick delivery of goods to users is a primary objective for holding inventories. This is especially true in terms of consumer goods.
Buffering against Uncertainty : Inventories are often held because either the demand for goods or the replenishment of goods is subject to uncertainty. Anticipated demand for products is often forecasted in various ways. Sometimes there is also uncertainty regarding supply; that is, how quickly can goods be replenished? Transportation, quality problems, excessive scrap, and supplier lead times are often
factors contributing to uncertainty for which inventory can compensate.
Providing Variety : Not only is there uncertainty regarding the timing of demand for goods, but there is also uncertainty regarding exactly what will be demanded. This is often the case where goods are available with various options, colors, or packaging. Inventories in a variety of configurations are therefore needed to adequately fulfill customer demands.
Operating efficiency
Inventories help make a manufacturing operation more productive in 4 ways:
- Inventories allow operations with different rates of production to operate separately and more economically;
- To level production, build anticipation inventory for sale in the peak periods. This would result in the following:
o Lower overtime costs,
o Lower hiring and firing costs,
o Lower training costs,
o Lower subcontracting costs,
o Lower capacity required.
By leveling production, manufacturing can continually produce an amount equal to the average demand. The advantage of this strategy is that the costs of changing production levels are avoided;
- Inventories allow manufacturing to run longer production runs, which results in the following:
o Lower setup cost per item. The cost to make a lot depends upon the setups cost and the run costs. The setup costs are fixed, but the run
costs vary with the number produced. If larger lots are run, the setup costs are absorbed over a larger number and the average unit cost is
lower,
o An increase in production capacity due to production resources being used a greater portion of the time for processing as opposed to
setup. If larger quantities are produced at one time, there are fewer setups required to produce a given annual output and thus more
time is available for producing goods. This is most important with bottleneck resources. Time lost on setup on these resources is lost
throughput and lost capacity;
- Inventories allow manufacturing to purchase in larger quantities, which results in lower ordering costs per unit and quantity discounts.
Inv conflict & Resolution
The objectives regarding inventories, indicated above, are often in conflict. Whether used to provide customer service or to achieve efficiencies in procurement or production, inventories conflict with management’s desire to minimize inventory investment. Long production runs by manufacturing operations tend to create large stocks of single products, whereas marketing organizations would often prefer stocks of a larger variety of products and options to serve a broad customer demand.
Large inventories also take up space in factories and distribution centers that is not only expensive to acquire and maintain, but also may lead to loss and confusion as congestion prevents adequate controls and physical storage
The problem is to balance inventory investment with the following:
- Customer service. The higher the inventory level, the higher customer service will be;
- Costs associated with changing production levels. Excess equipment capacity, overtime, hiring, training and layoff costs will be higher if production fluctuates with demand;
- Cost of placing orders. Lower inventories can be achieved by ordering smaller quantities more often, but this practise results in higher annual ordering costs;
- Transportation costs. Goods moved in small quantities cost more to move per unit than those moved in large quantities. However, moving large lots implies higher inventory.